Contents

Predicting Algerian Forest Fires with Machine Learning

Predicting Algerian Forest Fires with Machine Learning

from IPython.display import Image

Authors: Ingrid Chien, Johnson Du, Minori Jaggia, Leif Martin Saether Sunde

Introduction

Starting in June 2012, the Bejaia and Sidi-Bel Abbes regions of Algeria experienced numerous wildfires that likely resulted from a heat wave. The fires burned throuh Algeria’s pine and cork oak forests, damaging a total area of 295 square kilometers.

Purpose of Analysis

Do weather metrics in the Algerian regions determine the occureces of forest fires? How distinct are weather metrics for forest fires? How can we detect fires before they occur?

Our team uses machine learning to process features and predict whether or not a fire will occur based on significant attributes. Our model is based on data from Bejaia and Sidi-Bel Abbes, but we aim to build more robust and generalizable models that can help policy makers in different regions implement precautionary measures against fires before they strike.

Assumptions

In our analysis, we assume that the response variable is binary. The response variable is the class ‘fire’ or ‘not fire.’ We do not consider midway situations, such as fires that were close to ignition but utimately faded. We assume that our observations are unique instances with no extreme outliers. We also deduce that the samples are representative and large enough to make justifiable predictions.

The Data

Data Acquisition

The multivariate dataset is acquired from the UCI Machine Learning repository. It can be found at https://archive.ics.uci.edu/ml/datasets/Algerian+Forest+Fires+Dataset++.

The data contain a total of 244 instances for the two regions with 122 instances per region. There are 12 attributes, including date variables and weather metrics, that are measured from June 2012 to September 2012. Descriptions of the attributes can be found at the provided link. There are no missing values.

There are 2 repsonse classes, ‘fire’ and ‘not fire.’

Data Cleaning

The data is originally formatted as two stacked datasets where the top corresponds to Bejaia and the bottom correponds to Sidi-Bel Abbes. We combine them into one dataframe and create a ‘Region’ variable to distinguish regions. We reset the index and polish the column names for easy manipulation.

Exploratory Data Analysis

We first examine the correlation between all pairs of attributes except ‘date’ and ‘time’. We find that some variables are highly correlated with one another, such as BUI and DC. These findings are later reflected in our feature selection process in modeling to avoid multicollinearity.

Pairwise Correlations

Let us focus on the relationships for fire behavior indicies and fuel moisture codes. We expect to see correlations. For example, one fuel moisture code should heavily effect another fuel moisture code, as they capture similar information.

Image("figures/figure_1.png", width=600)
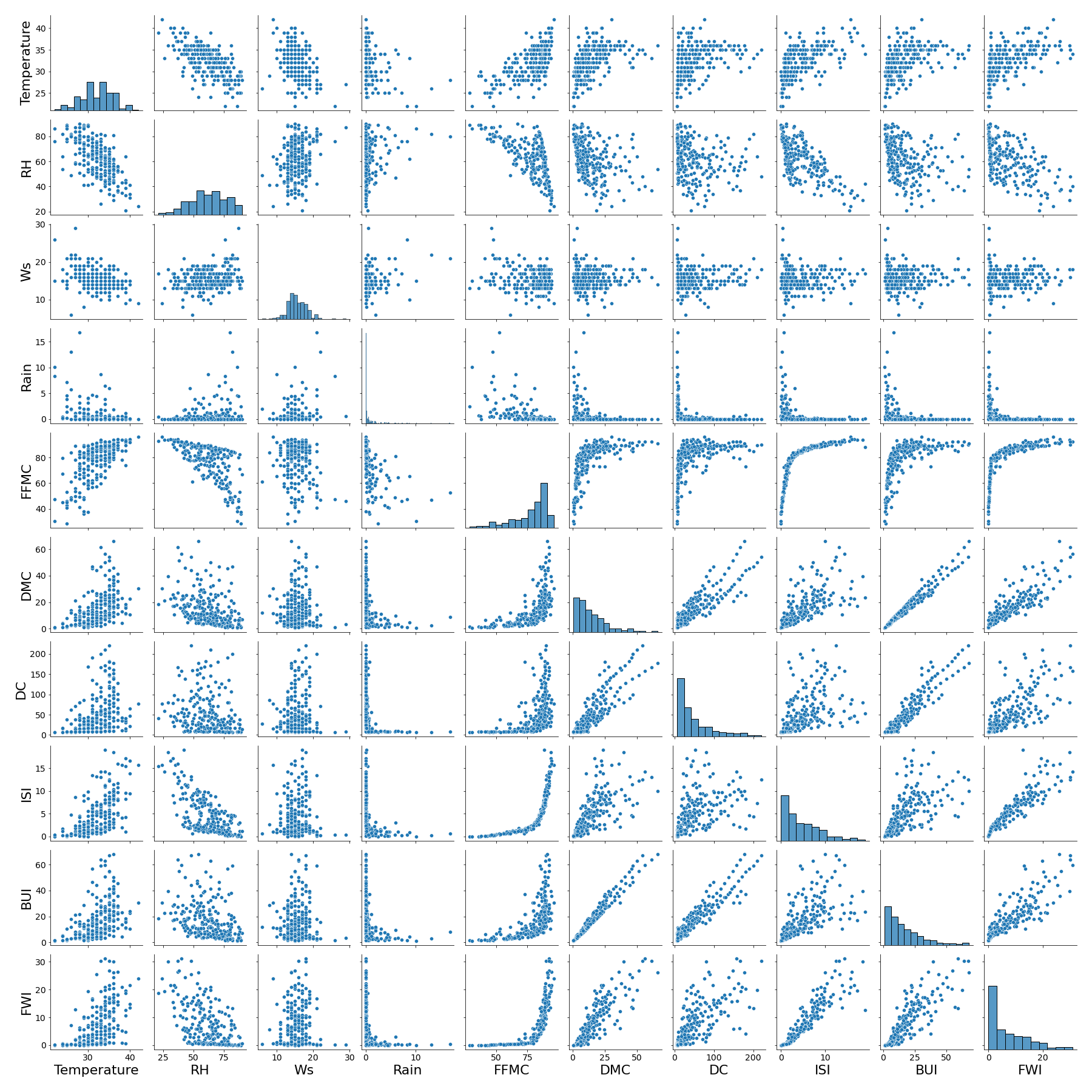
_images/main_10_0.png

Figure 1: Pairwise correlations between features of forest fire dataset

Fire Behavior Indices

As expected, the variables rougly follow linear relationships and show positive correlation. It is no surprise that, for example, higher FWI induces higher BUI if larger fires are likely to have large buildups.

Image("figures/figure_2.png", width=400)
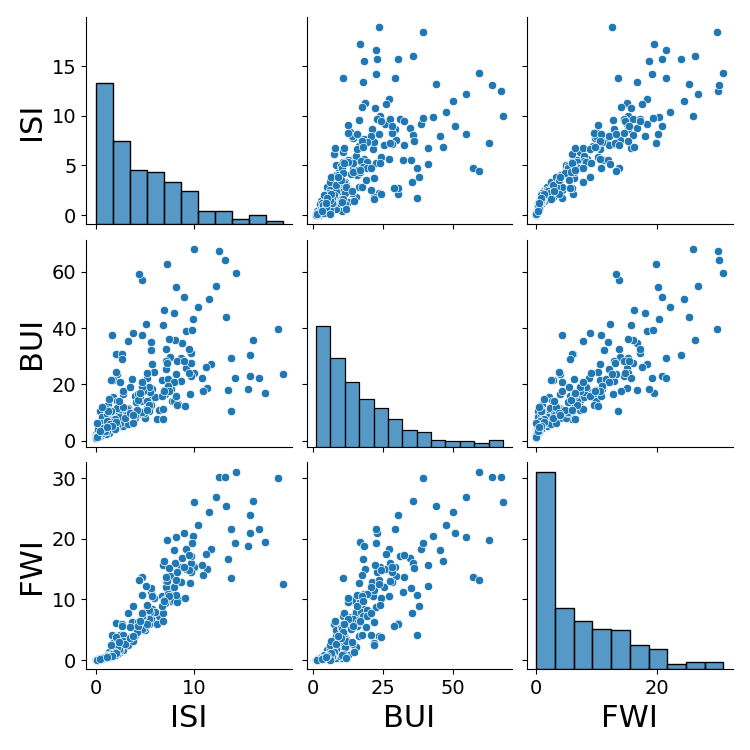
_images/main_13_0.png

Figure 2: Pairwise correlations for fire behavior indices

Fuel Moisture Codes

DMC and DC roughly follow a linear relationship. The remaining relationships seems to be logarithmic, though the curves are quite sharp. As FFMC increases, DC stays consistent until around 80 FFMC where the spread increasees greatly. The FFMC is an inverse measure of moisture content for easily ignited surface litter and other cured fine fuels. Thus, it makes sense that FFMC increases as DC increases.

Image("figures/figure_3.png", width=400)
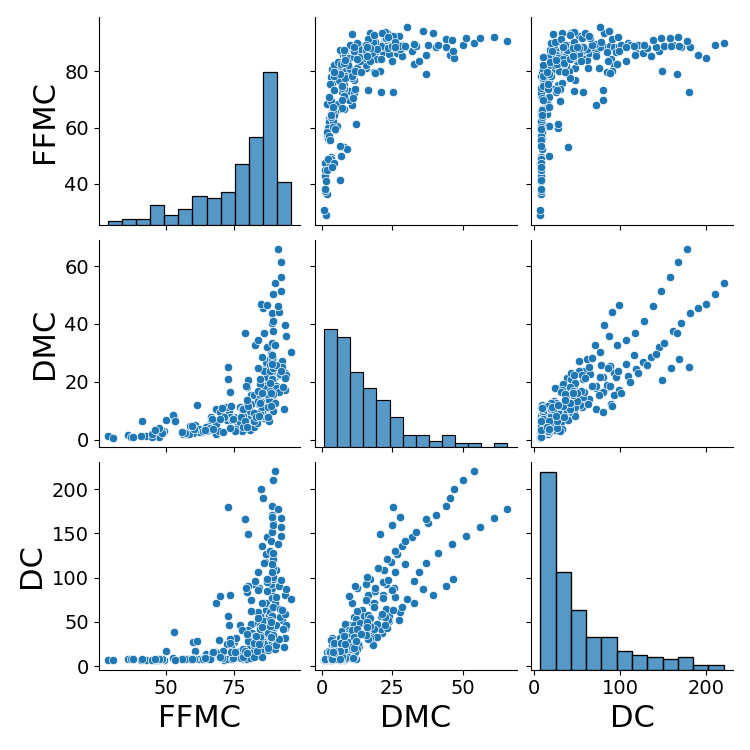
_images/main_16_0.png

Figure 3: Pairwise correlations for fuel moisture codes

FWI Distributions

Another interesting attribute is FWI. The distributions of FWI for ‘fire’ instances and ‘not fire’ instances drastically differ. If FWI is over about 8, then the data indicates we can be reasonably sure the instance is a ‘fire’.

Image("figures/figure_4.png", width=600)
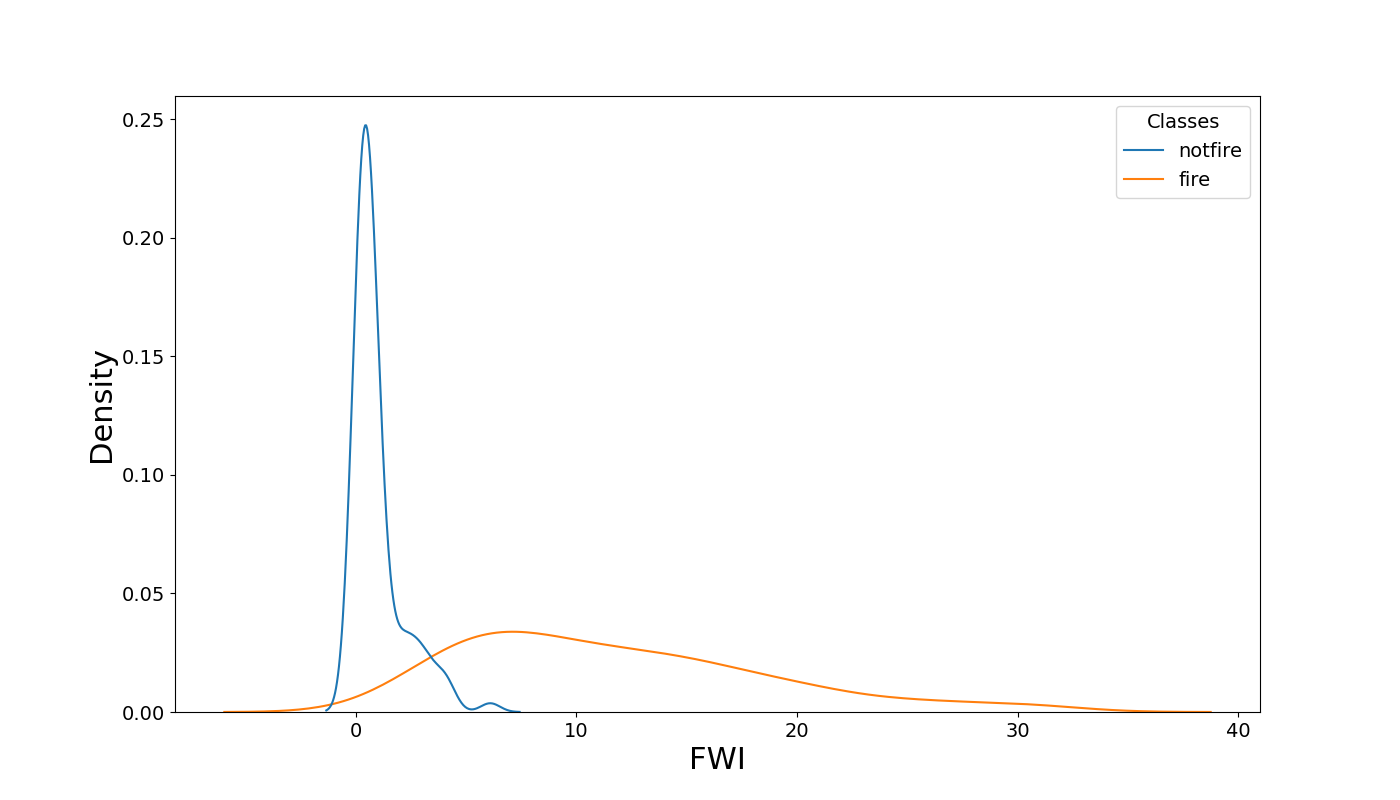
_images/main_19_0.png

Figure 4: Distribution of fire weather index (FWI) of different classes

Additional EDA shows that about half of the fires occured in July 2012. Also, there exists outliers in the ‘Rain’ attribute, but they are kept in the data because we assume consecutive days of heavy rain are natural.

Models

We build a random forest model and a logistic regression model to predict the occurence of forest fires.

Random Forest Model

Our grid search cross validation searches the model and performs 10-fold cross validation on combinations of hyperparameters. The hyperparameters we consider are the number of trees to grow, and the maximum depth of each tree. Considering that our data is small and we have a small amount of features, it is reasonable to guess that we won’t need a large number of trees, and we don’t need to grow them very deep.

During cross validation, we choose to evaluate the model based on recall because we prioritize penalzing false negatives. We want to avoid predicting no fire when there is actually a fire.

From the figure below, we conclude that recall is stable when we use more than 35 trees and that results are best when the trees are depth 1. The cross validation results shows that the best hyperparameter choices are 38 trees with maximum depths of 1.

Image("figures/figure_5.png",  width=800)
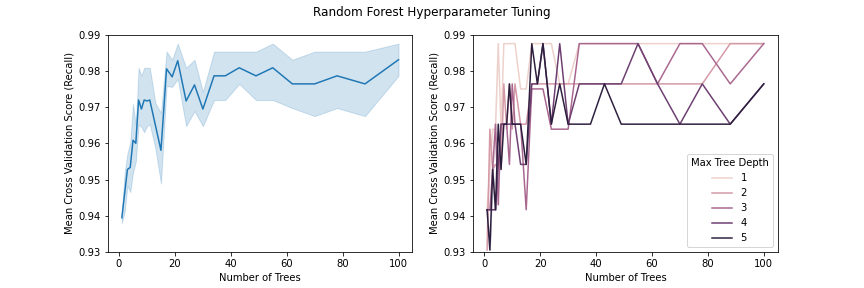
_images/main_23_0.png

Figure 5: (Left) Change in CV recall score as number of trees increase; (Right) CV recall score for different maximum tree depth and different number of trees

The confusion matrix shows that our random forest model has great performance. The accuracy is 100%! Can we do better or worse with simple logistic regression?

Image("figures/figure_6.png",  width=400)
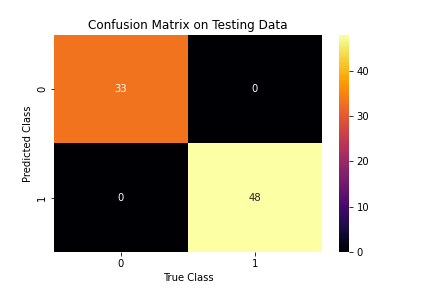
_images/main_26_0.png

Figure 6: Confusion matrix for random forest model

Accuracy: 1.0

Precision: 1.0

Recall: 1.0

Logistic Regression Model

By using logistic regression, we assume there is a possibility that the data can be linearly separated. Depending on which model does better, we make further assumptions about the nature of our data. If the random forest is superior, we believe the data is better suited for non linear algorithms.

With previous EDA, we find that that DMC, DC, and BUI and highly correlated with one another. Only DMC is kept to avoid multicollinearity. Notice how this step is skipped in the random forest model because the forest implicity performs feature subset selection.

We use logistic regression with l2 regularization and the ‘lbfgs’ solver. Our logistic regression model also has great performance, though there are a few more errors compared to the random forest model.

Image("figures/figure_7.png",  width=400)
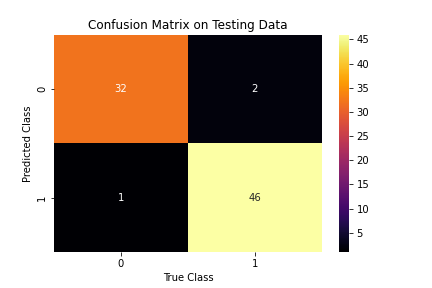
_images/main_31_0.png

Figure 7: Confusion matrix for logistic regression model

Accuracy: 0.9629629629629629

Precision: 0.9583333333333334

Recall: 0.9787234042553191

To better undestand the model, let us examine the area under the ROC curve, which plots true positive rates against false positive rates for different thresholds.

Amazingly, the area under the curve is close to 1! Our linear classifier is almost perfect, which leads us to believe the data can be linearly separated.

Image("figures/figure_8.png",  width=600)
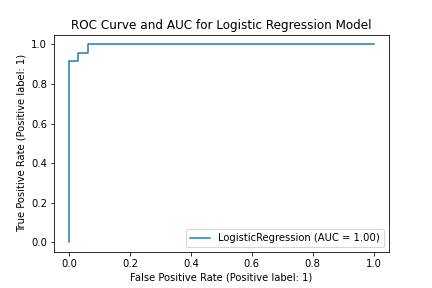
_images/main_34_0.png

Figure 8: ROC curve for logistic regression model

Interpreting Results and Model Comparison

Both models are extremely well-conditioned for the task of classifying forest fires. We display our scoring metrics below for easier comparison of the models. Even a simple logistic regression model with typical feature engineering achives a near perfect accuracy. Is it possible that the data is inherently good for classification? Perhaps Algerian forest firest have particularly distinct features that make them easy to distinguish from regular forest conditions. From EDA, we see that most fires occured in July, causing us to wonder if ‘month’ is a significant factor in determining fire occurence. We can examine the importances of each feature in prediction by looking at the coefficients from our logistic regression model. As seen below, the FFMC was the most powerful in prediction (we can compare directly since we normalized the data). This makes sense based on our EDA which showed that FFMC combines aspects of many of the other features and is therefore the most holistic predictor of fires. In fact, this means that an increase of 1 point in FFMC increases the odds of a forest fire by about 10%, which is quite considerable. Fire scientists can use FFMC as a north star metric in understanding fire probabilities.

The random forest outperforms the logistic model. This is expected because random forests are more expressive. The removal of correlated variables in the logistic model need not be the reason for poorer performance because they are calculated from kept features. The random forest succeeds by using a non linear split that cannot be represented by the logistic model.

Our models are conditioned to predict fires in regions of Algeria. It is unclear how the models will respond to forest fires in other locations. We aim to conduct further exploration by training our models with data from different locations with similar climates. We can monitor the models’ variances and ask the question: Are Algerian forest fires easier to predict than other forest fires?

Image("figures/figure_9.png",  width=400)
_images/main_37_0.png

Figure 9: Comparing metrics for random forest model and logistic regression model

Image("figures/figure_10.png",  width=200)
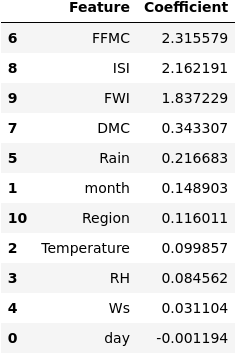
_images/main_39_0.png

Figure 10: Logistic regression model features coefficients

Author Contributions

Johnson Du

  • Responsible for data_cleaning.ipynb.

  • Responsible for the random forest classifier model (random_forest.ipynb, etc.)

  • Responsible for restructure_data() and evaluate_model() function in tools\utils.py.

  • Responsible for writing tests for the util functions.

  • Responsible for Makefile.

Ingrid Chien

  • Responsible for the logistic regression model (random_forest.ipynb, etc.).

  • Responsible for the normalize() and preprocess_data() functions in tools\utils.py.

  • Responsible for configuring tools as an installable package (pyproj.toml, setup.py, setup.config).

  • Responsible for writing project report in main.ipynb.

Minori Jaggia

  • Responsible for parts of EDA.ipynb

  • Responsible for environment.yml

  • Responsible for LICENSE.md

  • Responsible for parts of model comparison and interpretation in models.ipynb

  • Responsible for parts of creating jupyterbook, and configuring github actions

Leif-Martin Sæther Sunde

  • Responsible for parts of EDA.ipynb.

  • Responsible for parts of comparing results in models.ipynb.

  • Responsible for parts of README.

  • Responsible for binder support.

  • Responsible for parts of creating jupyterbook, and configuring github actions

next

Data Cleaning